Miscible Treatment

A serious problem in equation of state modelling is to establish a phase identity-independent \(K_{rh}(S_h,S_w)\) model which becomes a straight line when we approach the critical point. Otherwise the problem is unsolvable in this region as \(\partial(sat)/\partial(zmf) \Rightarrow\infty\) at the critical.

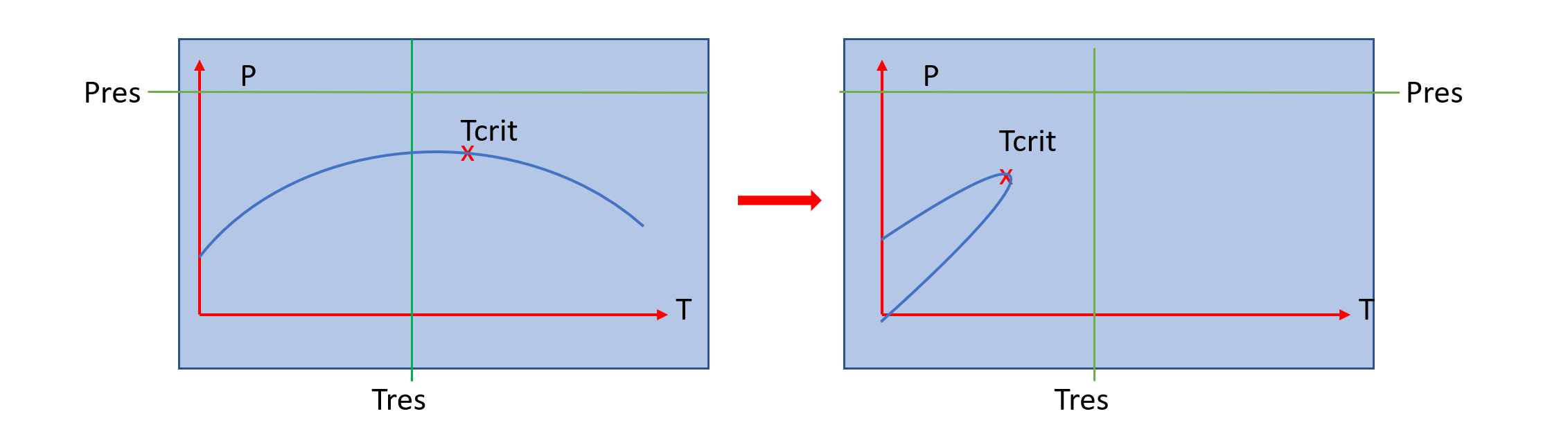
A further problem, even if the system does not approach the critical point, is that, in a miscible flood (such as when CO₂ invades hydrocarbon regions) the system phase envelope can move from right to left, so that a system can change from a liquid to a gas, without going through an intermediate two-phase state. This can produce a serious discontinuity which renders solving the non-linear equations very difficult:

The solution is to make the relative permeability and capillary pressure functions dependent on surface tension – which is reasonable, as we would expect zero capillary pressures and straight-line relative permeabilities in the case of zero interphase surface tension. Then we make the surface tension a function of the compositions of the phases. To do this we use a classical correlation for surface tension, the McLeod-Sugden expression [Sug24], which is a function of the component parachors, which become a new required set of input values.

The surface tension, \(\sigma\), computed by [Sug24], such that \(\sigma \Rightarrow 0\) as the oil and gas phase compositions converge, is used to define a miscibility fraction:

\[f_m=1-f_i, \; f_i= \left(\frac{\sigma}{\sigma_{ref}} \right)^P\]

Where \(\sigma_{ref}\) is the surface tension in some immiscible reference state at which the rel. perms are measured. P is a parameter that goes from 0.15 to 0.25 (taken equal to 0.25).

While an ‘oil’ fraction can be defined as:

\[f_o=\frac{T_c}{(T_c+T_{res})}\]

Where \(T_c\) and \(T_{res}\) are the critical and reservoir temperatures, respectively. So that \(T_c=T_{res}\), \(f_o=0.5\); if \(T_c>>T_{res}\) (critical above res temp), then \(f_o \Rightarrow 1\).

The gas fraction is simply taken as the complement of the oil fraction:

\[f_g=1-f_o\]

With \(f_o\) and \(f_g\), the rel. perm of each of the hydrocarbon phases is expressed as follows:

\[K_{rh} = f_o \, K_{ro} + f_g \, K_{rg}\]

Where

\[K_{rg}(S_g,S_w) = \frac{(S_o \, K_{rgo}(S_g) + S_w \, K_{rgw}(S_w))}{(S_o+S_w)}\]

Four tables are required: \(K_{row}\), \(K_{rog}\), \(K _{rgo}\) and \(K_{rgw}\). If these are not available, \(K_{row}\) is taken as \(K_{rgw}\).

\(K_{rog}\) and \(K_{rgo}\) are computed as:

\[K_{rog} = f_i K_{rog} (\mbox{scaled table val}) + f_m \, K_{rog} (\mbox{scaled straight line value}).\]

Finally, the cap press pressure goes like \(P_{cog} \sim f_i\) and vanishes with surface tension:

\[P_{cog}(\mbox{scaled}) = f_i \, P_{cog}(\mbox{table})\]

So, as \(f_m \Rightarrow 1\), \(f_i \Rightarrow 0\), criticals and cap pressure vanish.

The result is a much smoother system in the near-critical and miscible region. The hydrocarbon phase has properties which are functions of its composition, not its phase label.