Residual Trapping and Stranded Gas Saturation

In gas-water runs with relative permeability hysteresis, which simulate CO₂ storage in saline aquifers, it is possible to output a ‘stranded’ gas saturation. In hysteresis modelling, it is common to form a ’trapped’ non-wetting phase saturation as a function of the historical maximum non-wetting (gas) phase saturation. However, this is really the potentially trapped saturation – the saturation at which the gas mobility will fall to zero if the gas saturation is reduced. The stranded saturation, on the other hand, provides a measure of the extent to which the gas in the aquifer has actually become immobilised and thus stranded as its saturation has fallen.

The definition of the stranded gas saturation follows the residual trapping described by ref Snippe et al. [ST14], and is shown in the figure below:

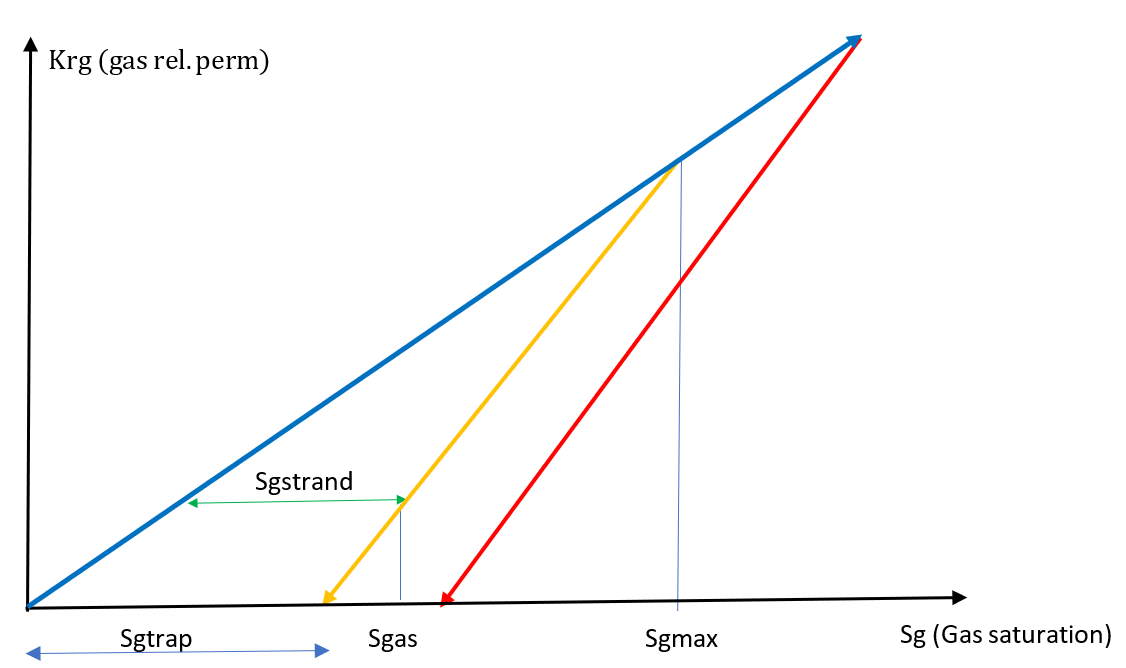
Suppose the gas saturation in an initially water-filled cell rises from zero to some \(S_{g, \mbox{max}}\) (a drainage process, blue line). If this reverses to an imbibition process the hysteresis models predict that the relative permeability traverses a scanning curve (yellow line). The relative permeability on the scanning curve falls to zero at the trapped saturation, Sgtrap. The trapped saturation is just a function of Sgmax.

Suppose we are at saturation \(S_{\mbox{gas}}\) on the scanning curve. The stranded gas saturation (\(S_{g,\mbox{strand}}\)) is defined as the horizontal interval between the drainage and scanning curve at \(K_{rg,\mbox{scan}}(S_{\mbox{gas}})\). The stranded saturation therefore interpolates between zero at \(S_{g,\mbox{max}}\) and \(S_{g,\mbox{trap}}\) when \(K_{rg} \rightarrow 0\). Therefore, while the \(S_{g,\mbox{trap}}\) contributes to the FGMTR (maximum potential residual trapping), \(S_{g,\mbox{strand}}\) contributes to FGMST (effective residual trapping).

Normally the critical gas on the drainage curve is zero, but if a critical drainage curve saturation exists it is added to the drainage-to-scanning-curve saturation interval.

Even if the gas mobility is zero, it is possible for the gas saturation to reduce – for example by compression or the gas dissolving in the water. The later is often an important effect in CO₂ storage cases. In that case, \(S_{g,\mbox{strand}}\) is reported as the minimum of the \(S_{g,\mbox{strand}}\) and the actual gas saturation – i.e., it is the actual stranded saturation, rather than the potential stranded saturation.