The Characteristic Curves Smoother

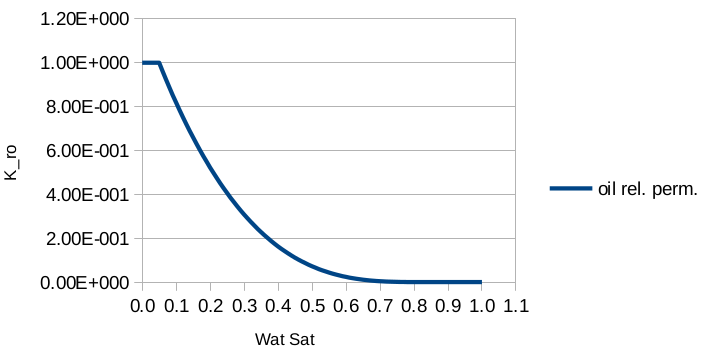
The smoothing functionality in proximity of the saturation points can greatly help convergence in some stiff numerical case. In practical terms, the smoothing interpolates the characteristic curves (saturation or relative permeability functions) close to the saturation points using a cubic polynomial which have to satisfy certain conditions. Let’s take for example an oil relative permeability curve described by the KROW MOD_BROOKS_COREY model with the following parameters:

\[\begin{split}\begin{split} &n_o &=3 \\ &S_{owcr} &=0.18 \\ &S_{wcr} &=0.05 \\ &k_{ro,max} &=1 \end{split}\end{split}\]

plotting the curve we have

The curve above features a derivative discontinuity when the oil saturation approaches its residual value. In this area the curve can be interpolated by a cubic polynomial, replacing the original expression with something smoother (see fig below).

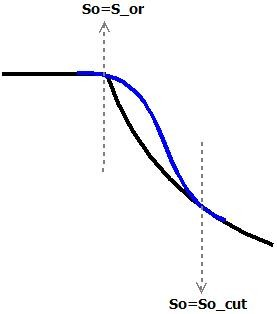
Interpolation by a cubic polynomial

The polynomial coefficients are defined imposing the same values of the original relative permeability curve and its derivative for \(S_o=S_{o,\mbox{cut}}\), and the maximum relative permeability value and null derivative for \(S_o=S_{or}\). \(S_{o,\mbox{cut}}\) must be very close to \(S_{or}\) to avoid significant modifications of the original curve: this tolerance is handle within the code imposing that \(S_{o,\mbox{cut}}\) diverges no more than \(1%\) from \(S_{or}\).